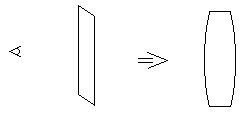
Pour représenter un objet 3D tel que nous le voyons, il faut rechercher l'intersection des rayons partant de l'oeil, passant par les points de l'objet et arrivant sur une sphère (une droite se projette en un arc de cercle, d'ellipse ou de parabole, comme sur une photographie prise au "grand angle"). Dans la pratique on utilise un plan de projection, plus facile à gérer et aux résultats proches (une droite se projette en une droite).
La méthode la plus simple est la projection parallèle. Elle est plus facile à opérer pour le dessin à la main mais ne rend pas un résultat conforme à la réalité, et n'est donc que peu utilisée avec les ordinateurs pour des rendus réalistes (une perspective ne nécessite pas beaucoup plus de calculs). Les rayons de projection sont tous parallèles et correspondent à une "vue de loin". Mais l'avantage de ces projections est que les projections de parallèles restent parallèles, et que les distances dans une direction donnée restent proportionnelles entre elles. Ce sera donc la projection utilisée pour les dessins techniques (mécanique en particulier).
Si le plan de projection est perpendiculaire à la direction de projection, on l'appelle projection axonométrique. Il suffit de tourner l'objet pour faire coïncider la direction de projection avec l'axe Oz, et ne plus dessiner que les x,y (z servant au problème des lignes cachées). Si les 3 axes sont raccourcis de façon égale (chacun à 120deg.), on l'appelle projection isométrique : rotation autour de Z de 45deg. puis de [theta] autour de Y (ou X) puis élimination de Z. [theta] ne vaut pas 45deg. car il faut ramener le point (1,racine(2)/2) sur l'axe et non (1,1)
X'
|
1
|
0
|
0
|
cos
T
|
0
|
sin
T
|
R
|
-R
|
0
|
X
|
||||||||||||||||
| Y'
|
=
|
0
|
1
|
0
|
* |
0
|
1
|
0
|
* |
R
|
R
|
0
|
* |
Y
|
avec
R = racine(2)/2
| |||||||||||
| 0
|
0
|
0
|
0
|
-sin
T
|
0
|
cos
T
|
0
|
0
|
1
|
Z
|
et
tg T = racine(2)
|
On l'appelle dimétrique si deux axes sont réduits de façon égale, trimétrique sinon. Le cas du dessin industriel est un ensemble de projections orthogonales dimétriques sur les plans X=0, Y=0, Z=0 (un des axes est réduit à 0).
Si le plan de projection n'est pas perpendiculaire à la direction de projection mais à un des axes, c'est une projection oblique. Les deux plus connues sont la projection cavalière (les longueurs suivant les 3 axes sont conservées) ou cabinet (les fuyantes sont raccourcies de moitié). On représente généralement les fuyantes à 30 ou 45deg., notons C le cosinus de cet angle, S son sinus :
X'
|
1
|
0
|
C
|
X
|
X'
|
1
|
0
|
C/2
|
X
|
||||||||||||||||||
| cavalière
:
|
Y'
|
=
|
0
|
1
|
S
|
* |
Y
|
cabinet
:
|
Y'
|
=
|
0
|
1
|
S/2
|
* |
Y
|
||||||||||||
| 0
|
0
|
0
|
0
|
Z
|
0
|
0
|
0
|
0
|
Z
|
On pourrait utiliser les projections sphériques, correspondant plus à ce que l'on voit réellement. En effet un grand rectangle dans un plan perpendiculaire à la direction de vision devrait se projeter sous forme d'un tonneau puisque la partie centrale, étant plus proche de l'oeil, doit paraître plus large que les extrémités.

Sauf lorsque l'on recherche des effets spéciaux, comme par exemple l'effet obtenu en photographie par un objectif grand angle, on se limitera aux projections planes. En effet nous trouvons plus réalistes les projections qui gardent rectilignes les droites (mais par contre ne garde pas parallèles des droites qui l'étaient initialement, comme le font les projections parallèles). Il y a deux méthodes possibles pour implanter ces perspectives (qui reviennent au même) :
soient : O l'oeil, V le point visé (sur le plan de projection), M le point à projeter :
On calcule en premier lieu la longueur de OM', avec M' projection de OM sur OV, à l'aide d'un produit scalaire. Le rapport des longueurs OM' et OV donne le point projeté sur le plan P. Il reste faut maintenant, à partir des coordonnées dans ce plan dans l'espace, trouver les coordonnées X,Y sur l'écran.

Il faut avant tout (à l'aide des matrices homogènes par exemple) déplacer la pièce (ou changer de repère), pour placer l'oeil en (0,0,0); puis la tourner pour placer le point visé sur l'axe Z (à la distance D), donc mettre V en position (0,0,D). Supposons M de coordonnées (x,0,z), et P en (x',0,D). Alors (d'après Thalès) : x'/x=D/z, donc x'=(D*x)/z.
Dans le cas général, on calcule la projection d'un point M (x,y,z) en un point P (x',y',D) en décomposant par les projections dans les plans Oxz et Oyz; donc x'=x.(D/z) et y'=y.(D/z)
Pour mettre V, de coordonnées initiales (X,Y,Z), sur l'axe Z : effectuons une rotation de T autour de Z puis de P autour de Y. or X2+Y2+Z2 = D2 (coordonnées sphériques).
| donc
|
cosP
= D/R
|
sinP
= racine(X2+Y2) /D
|
| cosT
= X/racine(X2+Y2)
|
sinT
= -Y/racine(X2+Y2)
|
On doit traiter une pyramide de vision, en général dans le repère déjà tourné pour effectuer la projection :
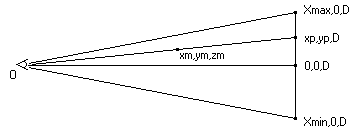
Le point M est visible si sa projection P est entre xmax et xmin, donc, d'après Thalès, xm/zm=xp/D, donc M est visible si :
xmin.zm/D <= xm <= xmax.zm/D et ymin.zm/D <= ym <= ymax.zm/D
Comme dans le plan, on peut tester la visibilité d'un segment en codifiant la visibilité des deux extrémités par 4 bits (haut, bas, droite, gauche).
Par exemple, calculons l'intersection d'un segment avec le plan supérieur :
|
x = t(x2
|
-x1)
+x1
|
| droite
: y = t(y2
|
-y1)
+y1 plan : y = ymax.z/D = A.z
|
|
z = t(z2
|
-z1)
+z1
|
ceci permet de trouver l'intersection (dans le segment si 0<=t<=1)
Rq : - Nos équations projettent aussi bien ce qui est devant l'oeil que ce qui est derrière. En DAO mécanique on n'a normalement rien derrière, ce qui n'est pas le cas en DAO architecture par exemple (on entre dans une pièce) ou simulation de vol (on évolue dans le décor, et de plus la visibilité peut être limitée). On doit alors traiter un tronc de pyramide de visibilité. On utilise un plan avant (par ex quelques cm devant l'oeil pour éviter les divisions par 0) et un plan arrière. On obtient deux conditions supplémentaires : zmin<=zm<=zmax. Il est facile de généraliser le clipping en utilisant 6 bits.
- On ne prévoit que de tester le clipping sur les segments. Ceci permet de ne pas tester tous les points générés, et de traiter facilement toutes courbes. Par exemple, en décomposant un cercle de l'espace en segments, uniquement projetés ensuite, on obtient automatiquement un tracé en ellipse sans écrire ni calculer nulle part son équation, ni besoins de tests de visibilité compliqués.
L'utilisateur donne le "parallélépipède utilisateur" (ses limites en x, y et z), les positions de l'oeil et le point visé (qui donne la direction de projection et la distance du plan). On calcule les projections des 8 coins extrêmes, ce qui permet de déterminer automatiquement une "fenêtre utilisateur" en 2D. L'utilisateur peut toujours donner une fenêtre papier, à condition que sa définition ne dépende pas des coordonnées utilisateur puisqu'il ne les connaît pas (en 2D).
Il faut évidement calculer les paramètres de projection (coefficients de la matrice) uniquement lors de la définition de la projection, et pas à chaque tracé de point ou de droite.
Remarque pour le tracé d'un cylindre en mode trait : on trace simultanément les deux cercles (par segments de droites en général), et on cherche les tangentes (points du cercle) les plus éloignées de l'axe. En traçant les cercles par pas de 10 degrés (36 tests), on obtient une précision suffisante (même si l'on trace plus précisément les cercles)